

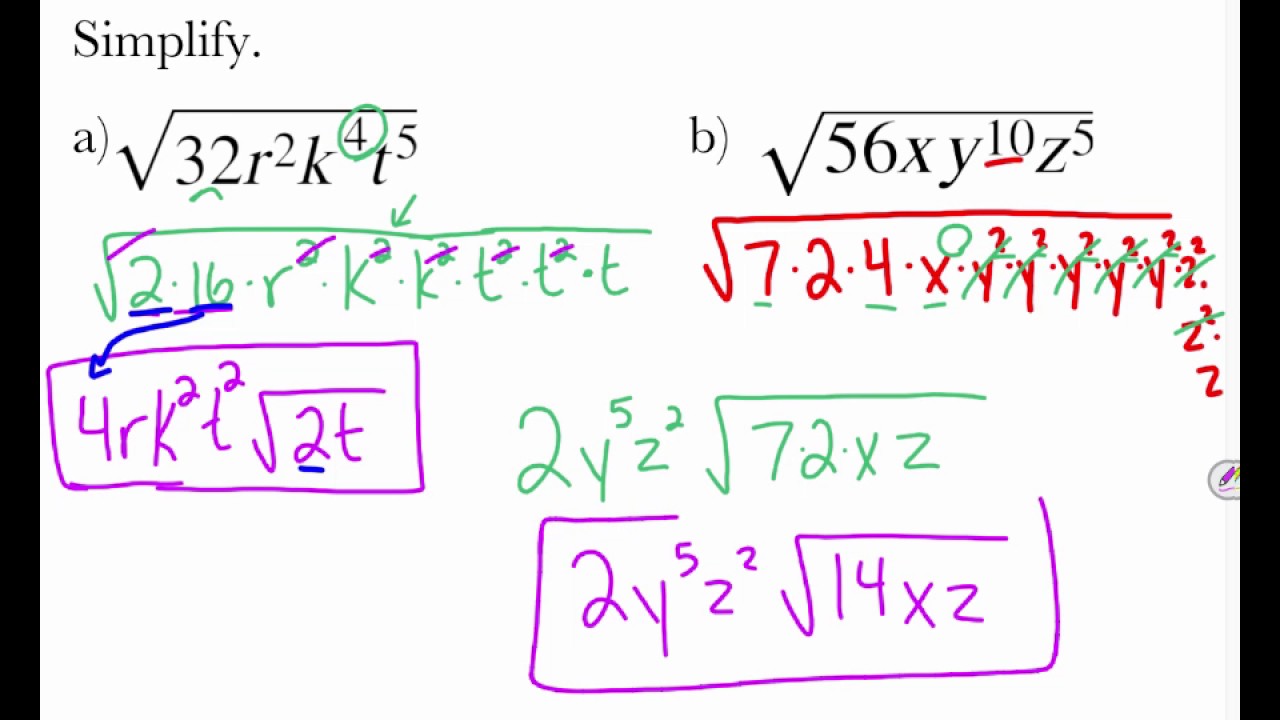
The corresponding of Product Property of Roots says that nab na nb. The properties we will use to simplify radical expressions are similar to the properties of exponents. Notice that in the examples in the table below, the denominator of the fractional exponent is the number 3. To simplify radical expressions, we will also use some properties of roots. Then, proceed like in the process of addition. Thus, the 2 y 2 will become 2 y 2 and 3 2 3 will become 3 2 3. Distribute the minus sign to the term in the subtrahend. Remember, cubing a number raises it to the power of three. Combine the like radicals in each expression before proceeding to subtraction. Let's look at some more examples, but this time with cube roots. In the table below we show equivalent ways to express radicals: with a root, with a fractional exponent, and as a principal root. Radicals and fractional exponents are alternate ways of expressing the same thing. Define \(\sqrt\) Write an expression with a fractional exponent as a radical.Add, subtract, multiply, divide, and simplify. Simplify radical expressions using fractional exponents and the laws of exponents Rationalize square root expressions and understand and use the concepts of negative and rational exponents.If there are fractions in the expression, split them into the square root of the numerator and square root of the denominator. Simplify radical expressions using factoring To simplify a radical expression, simplify any perfect squares or cubes, fractional exponents, or negative exponents, and combine any like terms that result.Use the product rule to rewrite the radical as the product of two radicals. Rewrite the radicand as a product of two factors, using that factor. Find the largest factor in the radicand that is a perfect power of the index. Convert expressions with fractional exponents to their radical equivalent Simplify a radical expression using the Product Property.Convert radicals to expressions with fractional exponents.Define and identify a radical expression.Radical Expressions and Fractional Exponents.Define and evaluate principal square roots.Simplification of algebraic expressions increases algebraic proficiency which is vital in any mathematics courses from calculus and beyond, including any applied courses.The pattern below is often called the difference of squares, and can be verified by applying the distributive property twice:.Knowledge of simplifying radical expressions is sufficient for being able to complete this exercise. Perform the indicated operations to solve. To find the domain, list all the values of the variable that, when. An excluded value in the function is any value of the variable that would make the denominator equal to zero. Simplifying Radical Expressions The simplest form of a radical expression is an expression that has: No perfect square factors other than 1 in the radicand. We have rational functions whenever we have a fraction that has a polynomial in the numerator and/or in the denominator. If the expression is already simplified, students should type it as it is. Simplifying Radical Expressions - Concept.
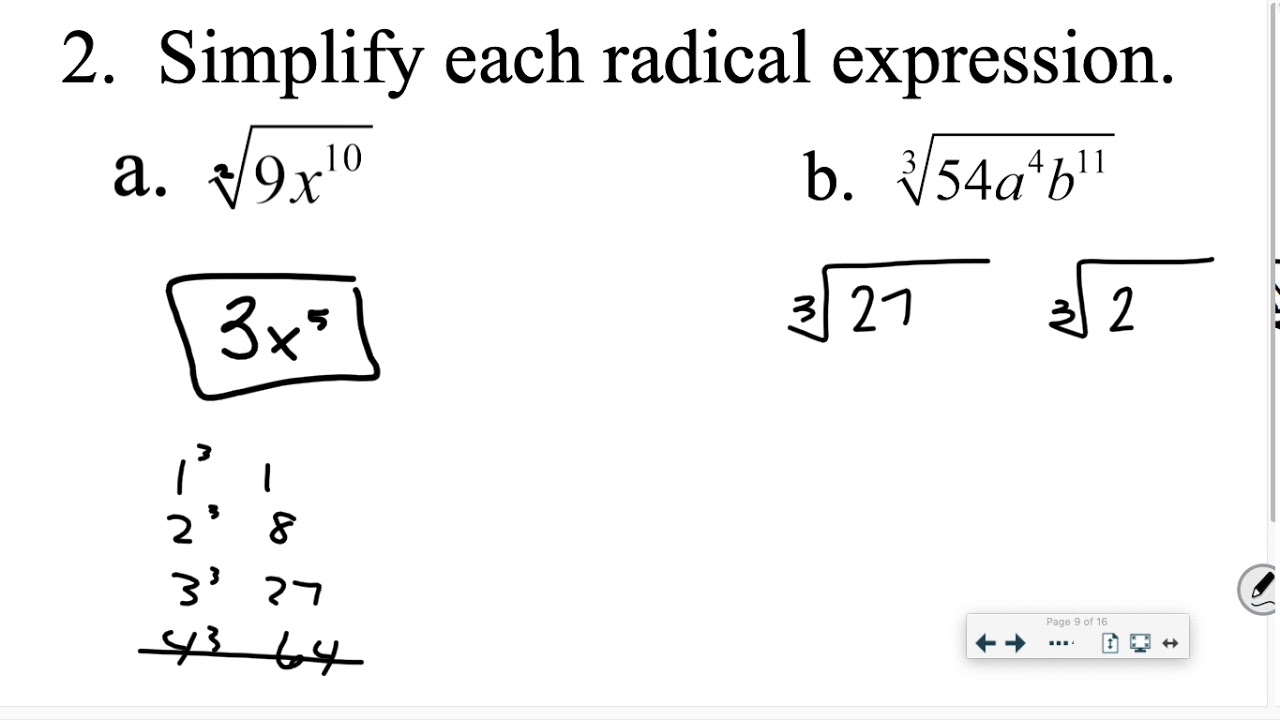
The student is asked to simplify the expression and type the answer in the space below. Perform the indicated operations to solve: This problem provides radical expressions with multiple terms.There is one type of problem in this exercise: This exercise simplifies practices simplifying expressions with multiple radical terms combined by addition, subtraction, multiplication, and/or division. This could include any combination of addition, subtraction, multiplication, and division of radicals. When we work with radicals, we’ll run into all different kinds of radical expressions, and we’ll want to use the rules we’ve learned for working with radicals in order to simplify them. The Simplify numerical radical expressions with multiple terms exercise appears under the Algebra II Math Mission. Rules we use for simplifying radical expressions.


 0 kommentar(er)
0 kommentar(er)
